Signed in as:
filler@godaddy.com
Signed in as:
filler@godaddy.com
A logical statement with a union or overlap copula and existential or non-existential quantification of its logical terms is called a Junctive.
Junctives are analogous to the eight forms of a monadic predicate with a bound variable as found in Predicate (First Order, Modern) Logic
Logical statements having only existentially or non-existentially quantified terms, that also have either union or overlap copulas are analogous to one of the eight forms of a monadic predicate with a bound variable in Predicate Logic
A logical statement in which the modal occasion of the copula is limited by the quantified triadic occasions of two logical terms is an overlap.
A junctive with an overlap copula is analogous to an existentially quantified monadic predicate.
A logical statement in which the modal occasion of the copula limits the quantified triadic occasions of two logical terms is a union.
A junctive with a union copula is analogous to a universally quantified monadic predicate.

ꓱα ∧ ∄β
Alpha is a variable (possible modality) and beta is a predicate (contingent modality). The occasion at the top center of the diagram is the Junctive rendered "there exists an alpha, alpha is a not-beta". This junctive is an accepted theorem (necessary modality).
The involution (De Morgan dual) of this Junctive is “∀α β(α)”

ꓱα ∧ ꓱβ
Alpha is a variable (possible modality) and beta is a predicate (contingent modality). The occasion at the top center of the diagram is the Junctive rendered "there exists an alpha, alpha is a beta". This junctive is an accepted theorem (necessary modality).
The involution (De Morgan dual) of this Junctive is “∀α ¬β(α)”

∄α ∧ ꓱβ
Alpha is a variable (possible modality) and beta is a predicate (contingent modality). The occasion at the top center of the diagram is the Junctive rendered "there exists an alpha, not-alpha is a beta". This junctive is an accepted theorem (necessary modality).
The involution (De Morgan dual) of this Junctive is “∀α ¬β(¬α)”

∄α ∧ ∄β
Alpha is a variable (possible modality) and beta is a predicate (contingent modality). The occasion at the top center of the diagram is the Junctive rendered "there exists an alpha, not-alpha is a not-beta". This junctive is an accepted theorem (necessary modality).
The involution (De Morgan dual) of this Junctive is “∀α β(¬α)”
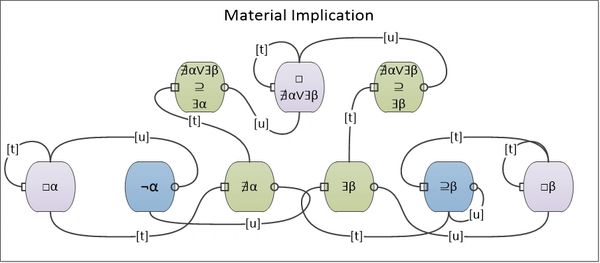
∄α ∨ ∄β
Alpha is a variable (possible modality) and beta is a predicate (contingent modality). The occasion at the top center of the diagram is the Junctive rendered "for all alpha, alpha is a not-beta". This junctive is an accepted theorem (necessary modality).
The involution (De Morgan dual) of this Junctive is “ꓱα β(α)”

∄α ∨ ꓱβ
Alpha is a variable (possible modality) and beta is a predicate (contingent modality). The occasion at the top center of the diagram is the Junctive rendered "for all alpha, alpha is a beta". This junctive is an accepted theorem (necessary modality).
The involution (De Morgan dual) of this Junctive is “ꓱα ¬β(α)”

ꓱα ∨ ꓱβ
Alpha is a variable (possible modality) and beta is a predicate (contingent modality). The occasion at the top center of the diagram is the Junctive rendered "for all alpha, not-alpha is a beta". This junctive is an accepted theorem (necessary modality).
The involution (De Morgan dual) of this Junctive is “ꓱα ¬β(¬α)”

ꓱα ∨ ∄β
Alpha is a variable (possible modality) and beta is a predicate (contingent modality). The occasion at the top center of the diagram is the Junctive rendered "for all alpha, not-alpha is a not-beta". This junctive is an accepted theorem (necessary modality).
The involution (De Morgan dual) of this Junctive is “ꓱα β(¬α)”